


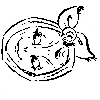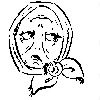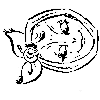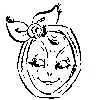


Jeder, der sich mit optischen Täuschungen beschäftigt, wird bald ihrer Faszination erliegen.
Die ersten drei (farbigen) animierten Gifs auf dieser Seite, zeigen uns Täuschungen, bei denen zweidimensionale Objekte Dreidimensionalität vorgaukeln. Im ersten Bild sehen wir scheinbar einen rotierenden Kegel. Im zweiten Bild scheint sich ständig etwas von uns wegzubewegen, das Auge gibt andauernd den Befehl zur Vergrößerung. Daraus kann man, wenn man auf eine etwas größere rotierende Spirale schaut und dann das Foto einer Blüte betrachtet, eine zweite Täuschung konstruieren: die Blüte scheint sich auszudehnen!
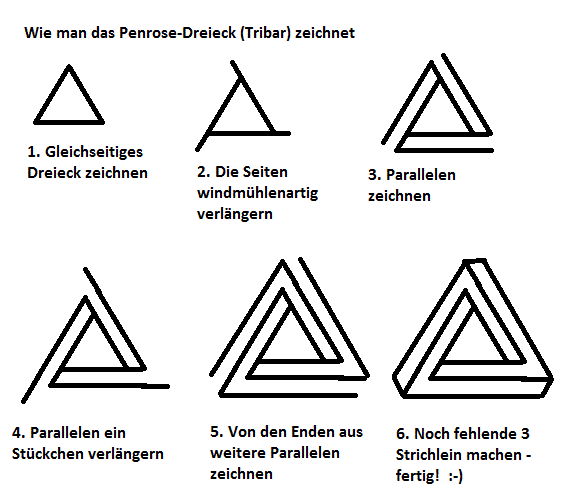
Das dritte farbige Gif zeigt uns schließlich das wohl berühmteste unmögliche Objekt: die unmögliche Dreibalkenkonstruktion oder impossible Tribar.
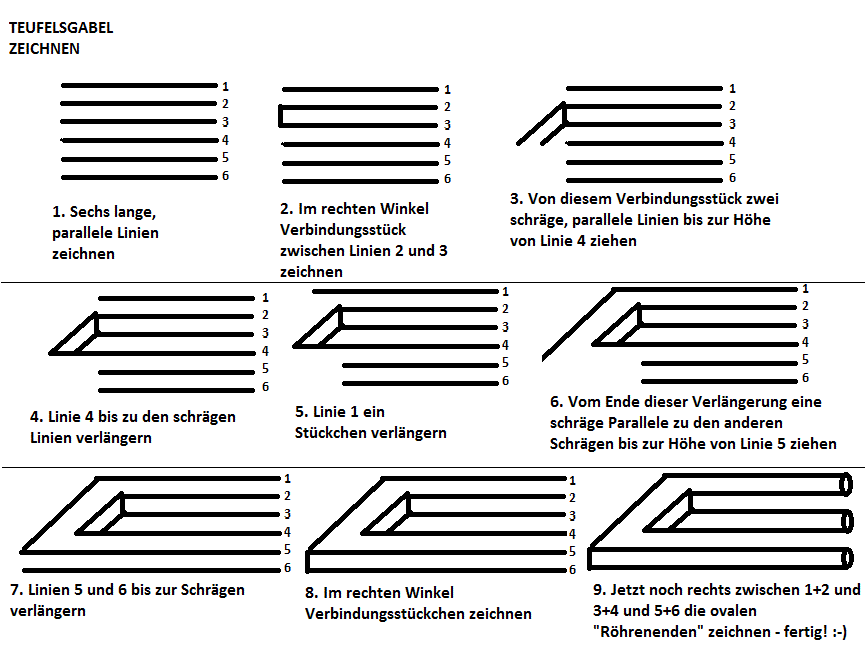
Hier Anleitungen zum Zeichnen des Tribars und der "Teufelsgabel":

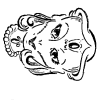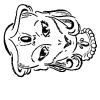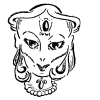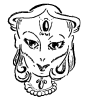
Weit älter als diese Objekte, sind die Vexierbilder, wie sie oben in den letzten vier animierten Gifs zu sehen sind: ein ganzes Bild oder Teil eines Bildes ergibt plötzlich ein neues Bild, wenn es auf die Seite gedreht, oder gar auf den Kopf gestellt wird
Hier das Bild, aus dem die oben gezeigten Gifs erstellt wurden:
Derartige Vexierbilder sind sehr alt und vermutlich die ätesten optischen Täuschungen, die man kennt. Folgende geometrische Täuschungen wurden im 19. Jahrhundert entdeckt:
Diese Täuschung wurde 1860 von Poggendorf beschrieben: die beiden diagonalen Striche scheinen voneinander versetzt zu sein. Verbindet man sie jedoch mit einem Lineal, sieht man, daß sie eine Gerade bilden!
Bei dieser Täuschung von Hering aus dem Jahr 1861 meint man, die beiden Geraden seien verbogen und somit auch nicht parallel, aber in Wirklichkeit sind sie gerade und auch parallel!
Bei dieser Täuschung von Müller-Lyer aus dem Jahr 1889 vermutet der Betrachter, daß die obere Strecke kürzer als die untere ist, aber beide sind, wie man durch Nachmessen leicht feststellen kann, gleich lang!
Diese Täuschung von Delboeuf aus dem Jahr 1892 ist im Prinzip das Gleiche, beide Strecken sind gleich lang!
Bei dieser Täuschung, ebenfalls von Delboeuf aus dem Jahr 1892, erscheint der linke innere Kreis kleiner, als der rechte äußere Kreis, aber beide sind, gleich groß!
Bei dieser Täuschung von Opel-Kundt aus dem Jahr 1895 scheint der linke Abstand zwischen den langen Strichen größer als der rechte Abstand, aber beide Abstände sind gleich groß!
Bei dieser Täuschung von Bitchener aus dem Jahr 1898 meint man, daß der linke inner Kreis kleiner als der rechte innere Kreis ist, aber beide sind gleich!
Die Diagonalen in den Rauten erscheinen verschieden lang bei dieser Täuschung von Sander aus dem Jahr 1920, aber beide Diagonalen sind gleich lang!
So viel zu optischen Täuschungen. Hier noch ein paar Seiten zum Thema im Web:
Hier eine deutsche Seite mit Optischen Täuschungen , darunter vielen mehrdeutigen Bildern (ziemlich lange Ladezeit).
Und noch eine englische Seite mit Optical Illusions .