Everyone, who occupies on optical illusions, soon will be fascinated by them.

The first three (coloured) animated Gifs on this page, show us illusions, where two-dimensional objects seem to be three-dimensional. In the first image, it seems like a rotating cone. In the second image, s. th. constantly seems to move away from us, so that the eye always gives the command to enlarge. On the base of this, one can create a second illusion: if you look on a bigger rotating spiral for a half minute and then look on the photo of a blossom, the blossom seems to expand.

Finally, the third coloured Gif shows us the probably famoust impossible object: the impossible Tribar.

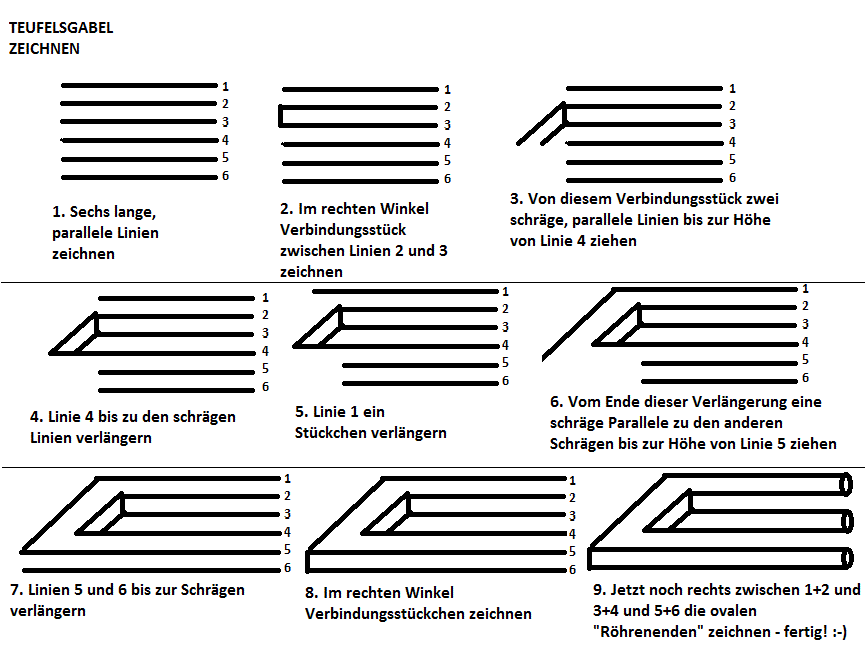
Here instructions how to draw the tribar and the "devil's fork":

A long way older than these objects, are the picture-puzzles, like we can see in the last four animated gifs above: a hole image or the part of an image leads to a new image, if you turn it, or put it upside down

Here the image, of which the above shown gifs were made.

These picture-puzzles are very old and presumably the oldest known optical illsuions. The following geometrical illusions heve been discovered in then 19th century:

This illusion has been described 1860 by Poggendorf: the both diagonal lines seem displaeced from each other. If one however connects them with a ruler, one sees, that they are on a straight line.

In this illusion by Hering of the year 1861 it seems, that the both straight lines are bend and therefore not parallel, but thy are really straight and also parallel!

In this illusion by Müller-Lyer of the year 1889 one supposes, that the distance above is shorter than the distance below, but both are, like one can find out by measuring, of equal length!

This illusion by Delboeuf of the year 1892 is quite the same, both distances are of equal length!

In this illusion, also by Delboeuf of the year 1892, the left inner circle seems to be smaller than the right outer circle, but both are of equal size!

In this illusion by Opel-Kundt of 1895 the left distance between the long strokes seems to be wider than the right distance, but both distances are the same!

In this illusion by Bitchener of 1898 it seems, that the left inner circle is smaller than the right inner circle, but both are the same!

The diagonals in the rhombs seem to be of different length in this illusion bei Sander of 1920, but they are of the same length!

That's all about optical illusion. Here some pages on the topic in the web:

Here a German page with Optical Illusions, among them many ambigous images (very long loading time).

And an english page with Optical Illusions .